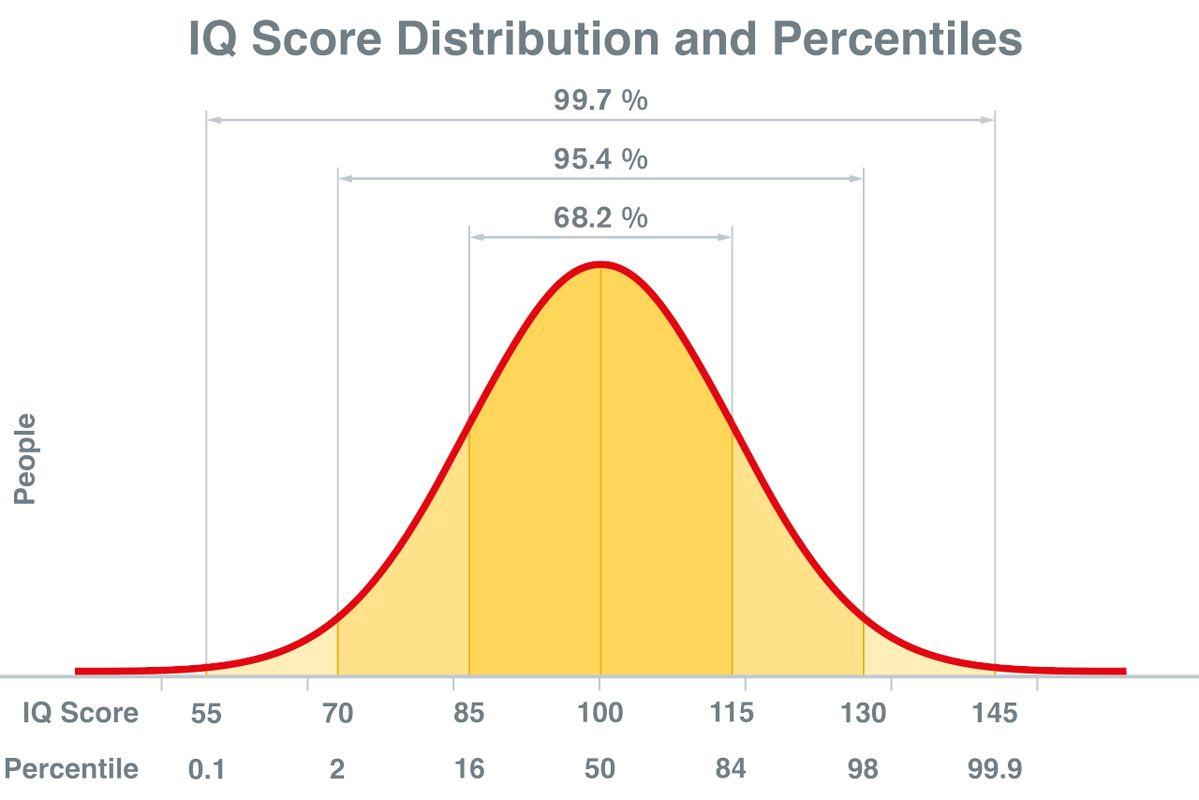
You've designed the perfect experiment. Your hypothesis is solid, your method is sound, and you're ready to collect data. But there's one question that could make or break everything: how many observations do you need?

Sample size isn't just a detail. It's the difference between detecting real effects and missing them completely. It determines whether your study has enough power to find what you're looking for. And when it comes to z-test calculators, getting it right is critical.

Let's talk about why sample size matters, how it affects your results, and how to figure out exactly how much data you need.

What Is Statistical Power?

Statistical power is the probability that your test will detect an effect when one really exists. Think of it as your test's ability to spot the truth.

Say you're testing a new drug that actually works. Power tells you the chance your study will show that it works. If your power is 80%, you have an 80% chance of detecting the drug's effect. But that also means a 20% chance of missing it, even though it's real.

High power is good. Low power is bad. You want your test to catch real effects, not miss them because you didn't collect enough data.

Most researchers aim for 80% power as a minimum. Some go for 90% or 95% if the stakes are high. Below 80%, you're playing a risky game where you might waste time and money on a study that can't deliver answers.

The Four Key Factors

Four things determine your statistical power. Change any one of them, and you change your ability to detect effects.

Sample size: More data gives you more power. This is the factor you control most directly.

Effect size: Larger effects are easier to detect. A 20% improvement is easier to spot than a 2% improvement.

Significance level (alpha): Usually set at 0.05. Lower this, and you need more power to compensate.

Variability in your data: More noise means you need more data to see through it.

These four factors work together. You can't change one without affecting the others. But sample size is usually the one you have the most control over.

Why Sample Size Makes or Breaks Your Z-Test

Z-tests compare sample statistics to expected values or compare two samples to each other. They rely on having enough data to work properly.

Too little data creates several problems:

You might miss real effects. With low power, your test can't distinguish signal from noise. You'll conclude there's no effect when one actually exists. This is called a Type II error or false negative.

Your estimates become unreliable. Small samples give you wide confidence intervals. Instead of "the effect is between 5% and 7%," you get "the effect is between -3% and 15%." That's not helpful.

The normal approximation breaks down. Z-tests assume your sampling distribution is approximately normal. With tiny samples, this assumption fails. Your p-values become inaccurate.

You waste resources. Running an underpowered study means you'll likely get inconclusive results. All that time and money spent for nothing.

On the flip side, too much data has its own issues. You'll detect tiny, meaningless effects as statistically significant. You'll spend more than necessary. And you might introduce more sources of error over the longer collection period.

The goal is finding the sweet spot: enough data to detect meaningful effects, but not so much that you're wasting resources.

Calculating Required Sample Size

Before you start collecting data, figure out how much you need. This process is called power analysis, and it keeps you from under- or over-collecting.

You need to specify four inputs:

Your desired power: Usually 0.80 or 0.90. How sure do you want to be that you'll detect an effect?

Your significance level: Usually 0.05. This is your Type I error rate, the chance of a false positive.

Your expected effect size: How big of a difference do you expect to see? This is the hardest to estimate but also the most important.

Your data's variability: Usually estimated from pilot studies or previous research.

With these inputs, you can calculate the minimum sample size needed.

For a z-test comparing two proportions, the formula gets complex. Most people use online calculators or statistical software instead of doing the math by hand. An Online Z test Calculator can quickly determine your needed sample size based on your specifications.

Effect Size: The Critical Input

Effect size is often the trickiest part of power analysis. It measures how big the difference or relationship is that you're trying to detect.

For z-tests comparing means, effect size is often expressed as Cohen's d: the difference between means divided by the pooled standard deviation. For proportions, it's just the absolute difference between the two proportions.

Small effect sizes need larger samples. If you're looking for a 1% difference in conversion rates, you'll need thousands of observations. If you're looking for a 10% difference, you might need only a few hundred.

How do you estimate effect size before collecting data?

Use previous studies: Look at similar research and see what effect sizes they found.

Run a pilot study: Collect a small amount of data to get a rough estimate.

Use domain knowledge: Subject matter experts can often give you reasonable ballpark figures.

Consider practical significance: What's the minimum effect size that would actually matter? There's no point detecting a 0.1% improvement if it wouldn't change your decisions.

Be conservative. If you're unsure, assume a smaller effect size. Better to slightly overcollect than to end up with an underpowered study.

Real Example: A/B Testing Sample Size

Let's say you're running an A/B test on your website. Your current conversion rate is 5%. You want to detect if a new design improves it to 6% (a 1 percentage point increase, or 20% relative improvement).

You want 80% power and will use alpha = 0.05 for a two-tailed test.

Plugging these numbers into a sample size calculator gives you about 3,850 visitors per group. That's 7,700 total visitors.

Now let's say you want to detect a smaller improvement, from 5% to 5.5%. Same power and alpha. You'll need about 7,800 per group, or 15,600 total. Double the effect size meant you needed half the sample size.

What if you increase your desired power from 80% to 90%? For the 5% to 6% scenario, you now need about 5,150 per group instead of 3,850. Higher power costs you more data.

These calculations show why you need to think carefully about what you're trying to detect before you start your test.

The Relationship Between Sample Size and Confidence Intervals

Sample size directly affects how precise your estimates are, which shows up in your confidence intervals.

A 95% confidence interval tells you: "I'm 95% confident the true value falls within this range." Wider intervals mean more uncertainty. Narrower intervals mean more precision.

The width of your confidence interval is roughly proportional to 1/√n. Double your sample size, and your interval width shrinks by about 30%. Quadruple it, and the width cuts in half.

This has practical implications. If your confidence interval for a conversion rate is 3% to 7%, you don't know if the new version is better or worse. But if it's 4.8% to 5.2%, you have a much clearer picture.

Larger samples give you tighter intervals, which means more actionable insights.

Common Mistakes in Sample Size Planning

Mistake 1: Not doing power analysis at all

Many people just collect whatever data they can get and hope it's enough. This is a recipe for wasted effort. Always calculate your needed sample size before starting.

Mistake 2: Using overly optimistic effect sizes

You hope for a big effect, so you assume you'll find one and calculate a smaller sample size. Then reality hits. Be realistic or even pessimistic about effect sizes.

Mistake 3: Ignoring multiple comparisons

Testing multiple outcomes or running multiple tests? You need to adjust for that. Either increase your sample size or use correction methods like Bonferroni.

Mistake 4: Stopping early when you see significance

Also called "peeking" or optional stopping. If you check your results repeatedly and stop when you hit p < 0.05, you inflate your Type I error rate. Decide your sample size upfront and stick to it.

Mistake 5: Treating power as all-or-nothing

Power isn't a threshold. A study with 78% power isn't fundamentally different from one with 80% power. These are guidelines, not hard rules.

When You Can't Get Enough Data

Sometimes you just can't collect as much data as you'd like. Budget limits, time constraints, or small populations can cap your sample size.

What do you do?

Be transparent about power: Calculate and report what power you actually achieved. Let readers know your study might miss smaller effects.

Focus on larger effects: If you can only detect big differences, that's what you should look for. Adjust your research question accordingly.

Use more sensitive designs: Paired tests, blocking, or stratification can increase power without adding sample size.

Consider Bayesian methods: They can squeeze more information from limited data, especially when you have prior knowledge.

Combine studies: Meta-analysis pools multiple small studies to achieve higher effective sample size.

Don't pretend your underpowered study is conclusive. But an underpowered study that acknowledges its limits is still better than no study at all.

Sample Size for Different Z-Test Scenarios

Different z-tests need different sample sizes.

One-sample z-test: You're comparing a sample mean to a known value. Generally needs smaller samples than two-sample tests because there's no sampling error in the comparison value.

Two-sample z-test: Comparing two independent groups. Needs larger samples because you have uncertainty in both groups.

Z-test for proportions: Sample size depends heavily on the proportions involved. Detecting differences near 0% or 100% requires enormous samples. Differences near 50% are easier to detect.

One-tailed vs. two-tailed: One-tailed tests have slightly more power for the same sample size, but you can only detect effects in one direction.

Each scenario has its own considerations. Use appropriate calculators or formulas for your specific case.

The Cost-Benefit Balance

Collecting data costs money, time, or both. You need to balance statistical rigor against practical constraints.

Think about the cost per observation. If each data point costs $1, collecting 10,000 observations costs $10,000. Is that worth it for your question?

Consider the value of information. A definitive answer might be worth a lot. An uncertain answer might be worth little. How much precision do you really need?

Sometimes a quick study with lower power makes sense. You get a directional answer fast. If it's promising, you follow up with a larger, more definitive study.

Other times, you only get one shot. A major product launch, a policy decision, or a medical trial needs to be right the first time. In these cases, err on the side of more data.

Make conscious choices about this tradeoff rather than letting it happen by default.

Monitoring Power During Your Study

Power analysis isn't just for planning. You can recalculate power during your study as you learn more.

Maybe your pilot estimate of variability was wrong. Maybe the effect size looks different than expected. You can update your calculations and adjust your target sample size if needed.

This is different from peeking at your p-value. You're not looking at whether the result is significant. You're checking whether your original assumptions still hold.

Some approaches:

Conditional power: Given your current data, what's the probability you'll reach significance if you continue to your planned sample size?

Predictive power: What's the probability you'll reach significance if the true effect equals your current estimate?

Futility analysis: Is the effect so small that even completing the study won't give you useful results?

These help you make informed decisions about whether to continue, stop early, or extend data collection.

Software and Tools

You don't need to calculate sample sizes by hand. Plenty of tools do it for you.

G*Power: Free, powerful, handles many test types. The go-to for many researchers.

R packages: pwr, WebPower, and others give you command-line control.

Online calculators: Quick and easy for common scenarios. Many specialized calculators exist for z-tests, t-tests, and proportions.

Statistical software: SPSS, SAS, Stata, and others have built-in power analysis functions.

Pick tools you're comfortable with and that handle your specific test type. Double-check calculations when the stakes are high.

Beyond Simple Power Analysis

Advanced topics can refine your approach:

Sequential testing: Allows you to stop early if results are clear, saving resources while maintaining error rates.

Adaptive designs: Adjust your sample size based on interim results in a principled way.

Non-inferiority and equivalence tests: Different power calculations when you're trying to show things are similar rather than different.

Bayesian sample size determination: Uses prior information and expected utility rather than power.

You don't need these for most studies. But they're available when standard approaches don't fit.

Making Sample Size Decisions

Here's a practical workflow:

Start by defining your research question clearly. What exactly are you trying to detect?

Estimate your expected effect size based on previous research, pilot data, or expert judgment.

Decide on your desired power (usually 80% or 90%) and significance level (usually 0.05).

Calculate your required sample size using appropriate tools.

Check if that sample size is feasible given your constraints.

If not feasible, adjust your expectations. Can you detect a larger effect size? Accept lower power? Modify your design?

Document your assumptions and calculations. Others need to see your reasoning.

Stick to your plan. Don't peek at results or stop early unless you've pre-planned for it.

This process keeps you honest and gives you the best chance of meaningful results.

Wrapping It Up

Sample size isn't something to guess at or ignore. It determines whether your z-test can actually answer your question.

Underpowered studies waste resources and miss real effects. Overpowered studies waste resources on unnecessary precision. Getting it right requires planning.

Do power analysis before you start. Be realistic about effect sizes. Consider your constraints. Use appropriate tools. And stick to your plan.

The extra time spent planning your sample size pays off in studies that actually deliver useful answers. That's time well spent.

Frequently Asked Questions

What's the minimum sample size for a z-test?

The traditional rule is 30 observations per group, but this depends on your population distribution and the effect you're trying to detect. Normal populations can work with smaller samples. Skewed populations need more. Power analysis gives you the real answer for your specific situation.

Can I increase my sample size if my results aren't significant?

No, not without careful consideration. Deciding to collect more data based on seeing non-significant results inflates your Type I error rate. If you want the option to extend your study, plan for it upfront using sequential testing methods.

How does sample size affect Type I and Type II errors?

Sample size directly affects Type II error (missing real effects) but doesn't change Type I error rate (false positives). Larger samples reduce Type II errors and increase power. Your significance level (alpha) controls Type I errors regardless of sample size.

Is 80% power always enough?

Eighty percent is a common standard, but not universal. Medical trials often use 90% or higher. Exploratory studies might accept 70%. Consider the consequences of missing an effect. High stakes call for higher power.

What if my pilot study shows a different effect size than expected?

Pilot studies give rough estimates, not precise ones. Small pilots have high uncertainty. Use them as guidance but stay conservative. If possible, use multiple sources of information to estimate effect sizes rather than relying on one small pilot.

How do I handle multiple outcomes or comparisons?

Multiple testing increases your chance of false positives. Either adjust your significance level (like using Bonferroni correction) or increase your sample size to maintain power after adjustment. Or designate one primary outcome and treat others as secondary.